TRIÁNGULOS RECTÁNGULOS
Posee un ángulo recto, es decir, que la
medida de uno de sus ángulos es de 90°, y los otros dos son ángulos agudos. -
Los dos lados que se intersecan y forman el ángulo recto se denominan catetos y
el lado que esta frente al ángulo recto se denomina Hipotenusa y es el lado con
mayor longitud.
Para determinar uno de los tres lados se
utiliza el teorema de Pitágoras
Teorema de Pitágoras
El teorema de
Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la
longitud de la hipotenusa es igual a la suma de los cuadrados de las
respectivas longitudes de los catetos, es decir, al elevar al cuadrado la
medida de la hipotenusa y al sumar al cuadrado las medidas de los catetos se
forma una igualdad. Este teorema se expresa con la siguiente formula C2
+ C2 = H2 y se representa gráficamente
Calcular el lado c del triángulo
rectángulo.
Hay que calcular un cateto por lo tanto
debemos despejar el teorema de Pitágoras
Reemplazamos los valores de la hipotenusa
y el cateto
TALLER 6
1.
Calcula el cuadrado de
los tres lados de estos triángulos y comprueba en cuál de ellos se cumple el
teorema de Pitágoras.
2.
3.
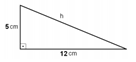
Halla la medida, en
centímetros, de la hipotenusa de un triángulo rectángulo, cuyos catetos miden 5
y 12 centímetros.
4.
Una letra “N” se ha construido
con tres listones de madera; los listones verticales son 20 cm y están separado
15 cm. ¿Cuánto mide el listón diagonal?
5.
6.
Al atardecer, un árbol proyecta una sombra de 2,5 metros de
longitud. Si la distancia desde la parte más alta del árbol al extremo más
alejado de la sombra es de 4 metros, ¿Cuál es la altura del árbol?
8. Una rampa tiene una longitud horizontal de 84 kilómetros y un altura de 13 km. ¿Cuál es la longitud de la rampa?
9.
10. ¿Cuál
es la distancia entre los puntos A y B?
RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO AGUDO EN TRÁNGULOS RECTÁNGULOS.
Para definir las razones
trigonométricas del ángulo ∝, correspondientes al vértice A, se parte de un triángulo
arbitrario que contiene este ángulo.
Un triángulo rectángulo que se
usará en lo sucesivo es:
La hipotenusa (h): es el lado
opuesto al ángulo recto, o lado de mayor longitud en el triángulo rectángulo.
El cateto opuesto (C.O.): es el
lado opuesto al ángulo ∝.
El cateto adyacente (C.A): es el
lado contiguo al ángulo ∝.
Tenga en cuenta que la suma de
los ángulos internos de un triángulo suma 180°, es decir 1π rad. Y la suma de los dos ángulos no rectos en un
triángulo rectángulo suman 90°
Seno (Sen∝):
Es la relación entre la longitud del cateto opuesto y la longitud de la hipotenusa.
coseno (Cos∝):
Es la relación entre la longitud
del cateto adyacente y la longitud de la hipotenusa.
Tangente (Tan∝):
Es la relación entre la longitud
del cateto opuesto y la longitud del cateto adyacente.
Ejemplo
3:
Calcular seno, coseno y tangente
del ángulo α, el otro ángulo.
Con
la calculadora científica realizar el siguiente procedimiento.
1.
Digitar las teclas shif y sin
2.
Digitar el valor obtenido en
proceso (en este caso 0,48) y luego dar igual 28,68
Con la calculadora científica realizar el siguiente procedimiento.
1.
Digitar las teclas shif y cos
2.
Digitar el valor obtenido en
proceso (en este caso 0,876) y luego dar igual 28.83
Tangente
Con
la calculadora científica realizar el siguiente procedimiento.
1.
Digitar las teclas shif y tan
2.
Digitar el valor obtenido en
proceso (en este caso 0,547) y luego dar igual 28.67
Ejemplo 4:
1.
Digitar la tecla sin
2.
Digitar el valor del ángulo 40 y
luego dar igual 0,6427 (tomamos 4 cifras después de la coma)
Reemplazamos los valores y tenemos
Despejamos el cateto opuesto
Luego calculamos el cateto
adyacente
En este caso lo primer que
hacemos es calcular el coseno de 40°, para esto digitamos en la calculadora:
1.
Digitar la tecla cos
2.
Digitar el valor del ángulo 40 y
luego dar igual 0,7660 (tomamos 4 cifras después de la coma)
Reemplazamos los valores y tenemos
Despejamos en cateto adyacente
TALLER 7
Calcular las razones trigonométricas de los
siguientes triángulos rectángulos, calcular el otro ángulo agudo y dibujarlo
con las medidas exactas. (Revisar ejemplo 3)
|
Cateto adyacente |
Cateto opuesto |
Hipotenusa |
|
7cm |
9 cm |
11,40 cm |
|
12,5 cm |
6,3 cm |
14 cm |
|
6,4 cm |
7 cm |
9,48 |
|
10 cm |
7,2 cm |
12,32 cm |
|
7,3 cm |
8,6 |
11,28 cm |
|
8,4 cm |
12 cm |
14,65 cm |
|
6, 5 cm |
4,7 cm |
8,02 cm |
|
5,6 cm |
5,6 cm |
7,92 cm |
|
Cateto
adyacente |
Cateto
opuesto |
Hipotenusa |
|
5 cm |
2,5 cm |
5,59 cm |
|
7,5 cm |
9,5 |
12,10 cm |
|
8,4 cm |
5 cm |
9,78 cm |
|
12 cm |
6 cm |
13,42 cm |
|
7,8 cm |
10,5 |
13,08 cm |
|
9,4 cm |
8,3 cm |
12,54 cm |
|
3, 5 cm |
3,5 cm |
4,95 cm |
|
11,6 cm |
9,5 cm |
14,99 cm |
TALLER 8
Calcular las razones trigonométricas de los
siguientes triángulos rectángulos, calcular el otro ángulo agudo. (Ejemplo 4)
|
Cateto adyacente |
Cateto opuesto |
Hipotenusa |
Ángulo α |
|
11 cm |
|
|
25° |
|
|
4 cm |
|
32,4° |
|
|
|
8 cm |
23° |
|
12, 4 cm |
|
|
39° |
|
|
5,7 cm |
|
63° |
|
|
|
16,4 cm |
18° |
|
3,5 cm |
|
|
26° |
|
|
8 cm |
|
45° |
|
|
|
14 cm |
30° |
|
|
|
18 cm |
65° |
|
4,7 cm |
|
|
48° |
|
|
11,6 cm |
|
72° |
|
|
32 cm |
|
16° |
|
27cm |
|
|
34° |
|
|
|
42 cm |
46,3° |
|
7,8 cm |
|
|
70° |
|
|
21 cm |
|
27° |
|
|
|
31,7 |
34° |
|
|
8,6 cm |
|
59° |
|
9,5 cm |
|
|
18,5° |
|
|
12,6 cm |
|
43,8° |
|
|
|
29,5 cm |
27° |

















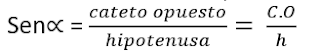




















No hay comentarios.:
Publicar un comentario